Learning DSA 3 (Binary Tree-1)

Catalan Number: ( standard problem for BST )

Catalan Numbers Series: 1,1,2,5,14,.........

nth Catalan Number using Recursion: Catalan numbers satisfy the following recursive formula,

C0=C1=1 then Cn will be:

Cn = C(i) + C(n-i-1) for i=0 to n-1 & n>=2

Time Complexity: O(n²)
Auxiliary Space: O(n)
nth Catalan Number using Binomial Co-efficient: Catalan numbers satisfy the following Binomial formula for nth term Cn,

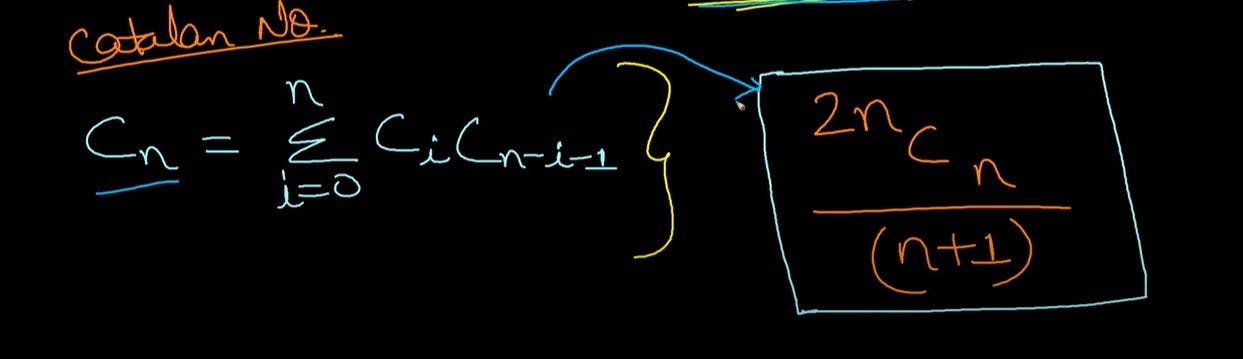
Standard problem for BST
1. To count the number of possible BST's with n Keys
2. To count the number of FullBT's with n+1 leaves

Fibonacci Number: ( standard problem for Recursion )

Fibonnacci Numbers series: 0,1,2,3,5,7,.............

nth Fibonnacci Number using Recursion: Formula,

f0=0, f1=1 then fn = f(n-1) + f(n-2)

nth Fibonnacci Number using DP: fn[i] = fn[i-1] + fn[i-2];

All possible problems on this: https://leetcode.com/discuss/study-guide/1854405/9-fibonacci-algorithms-the-most-complete-solutions-all-in-one-easy-to-understand

Binomial Co-efficient of n, k (nCk = C(n, k):

initial conditions, C(0, 0)=C(n, 0)=C(n,n)=1

FOR k>n, C(n, k)=C(n, n-k)
using RECURSION: C(n, k) = C(n-1, k-1) + C(n-1, k)

Time Complexity: O(n*max(k,n-k))

Auxiliary Space: O(n*max(k,n-k))
using DP: C[i][j] = C[i-1][j-1] + C[i-1][j] (2D array)

Trees Introduction:

Binary Tree vs Binary Search Tree:

S. No.	Basis of Comparison	BINARY TREE	BINARY SEARCH TREE
1.	Definition	BINARY TREE is a nonlinear data structure where each node can have at most two child nodes.	BINARY SEARCH TREE is a node based binary tree that further has right and left subtree that too are binary search tree.
2.	Types	Full binary tree, Complete binary tree, Extended Binary tree and more	AVL tree, Splay Tree, T-trees and more
3.	Structure	In BINARY TREE there is no ordering in terms of how the nodes are arranged	In BINARY SEARCH TREE the left subtree has elements less than the nodes element and the right subtree has elements greater than the nodes element.
4.	Data Representation	Data Representation is carried out in a hierarchical format.	Data Representation is carried out in the ordered format.
5.	Duplicate Values	Binary trees allow duplicate values.	Binary Search Tree does not allow duplicate values.
6.	Speed	The speed of deletion, insertion, and searching operations in Binary Tree is slower as compared to Binary Search Tree because it is unordered.	Because the Binary Search Tree has ordered properties, it conducts element deletion, insertion, and searching faster.
7.	Complexity	Time complexity is usually O(n).	Time complexity is usually O(logn).
8.	Application	It is used for retrieval of fast and quick information and data lookup.	It works well at element deletion, insertion, and searching.
9.	Usage	It serves as the foundation for implementing Full Binary Tree, BSTs, Perfect Binary Tree, and others.	It is utilized in the implementation of Balanced Binary Search Trees such as AVL Trees, Red Black Trees, and so on.

Traversals in Binary tree:

A Tree Data Structure can be traversed in following ways:

Depth First Search or DFS
1. Inorder Traversal (L, R, Ri)
2. Preorder Traversal (R, L, Ri)
3. Postorder Traversal (L, Ri, R)

Level Order Traversal or Breadth First Search or BFS
1. Boundary Traversal : “20 8 4 10 14 25 22”
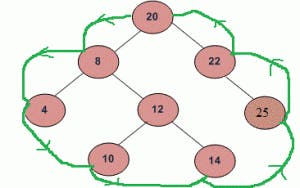
2. Diagonal Traversal :

Diagonal Traversal of binary tree : 8 10 14 3 6 7 13 1 4

Problems tried:

https://leetcode.com/problems/unique-binary-search-trees/description/

Too less, but worked

Sources: https://www.youtube.com/watch?v=CMaZ69P1bAc
https://www.geeksforgeeks.org/